Audit sampling: Get started

Koen Derks

Source: vignettes/articles/audit-sampling.Rmd

Introduction

Welcome to the ‘Audit sampling’ vignette of the jfa package. This page provides a straightforward guide to the functions in the package that are designed to facilitate statistical audit sampling. Specifically, these functions implement standard audit sampling techniques to calculate sample sizes, select items from a population, and evaluate the misstatement in a data sample compliant with international standards on auditing (American Institute of Certified Public Accountants (AICPA), 2021; International Auditing and Assurance Standards Board (IAASB), 2018; Public Company Accounting Oversight Board (PCAOB), 2020). The package allows enables to specify a prior probability distribution to conduct Bayesian audit sampling using these functions.

Functions and intended usage

Below you can find an explanation of the available functions in jfa, sorted by their occurrence in the standard audit sampling workflow.

Creating a prior distribution

The auditPrior() function is used to specify a prior distribution for Bayesian audit sampling. It enables formal translation of pre-existing audit information into a prior distribution or complete customization of the prior distribution. The function returns an object which can be used with associated summary() and plot() methods. Objects returned by this function can also be used as input for the prior argument in other functions. Additionally, these objects have a corresponding predict() method to generate the predictions of the prior distribution on the data level.

For additional details about this function, please refer to the function documentation on the package website.

Example usage:

# Beta prior based on inherent risk (70%) and control risk (50%)
prior <- auditPrior(
  method = "arm", likelihood = "binomial",
  materiality = 0.05, ir = 0.7, cr = 0.5
)
summary(prior)
## 
##  Prior Distribution Summary
## 
## Options:
##   Likelihood:                    binomial 
##   Specifics:                     ir = 0.7; cr = 0.5; dr = 0.1428571 
## 
## Results:
##   Functional form:               beta(α = 1, β = 21) 
##   Mode:                          0 
##   Mean:                          0.045455 
##   Median:                        0.032468 
##   Variance:                      0.0018865 
##   Skewness:                      1.7442 
##   Information entropy (nat):     -2.0921 
##   95 percent upper bound:        0.13295 
##   Precision:                     0.13295

Planning a sample

The planning() function is used to calculate a minimum sample size for audit samples. It allows the specification of approval conditions for the sample with respect to performance materiality or precision. The function returns an object which can be used with associated summary() and plot() methods. To perform Bayesian planning, the input for the prior argument can be an object returned by the auditPrior() function, or an object returned by evaluation()$posterior.

For additional details about this function, please refer to the function documentation on the package website.

Example usage:

# Poisson likelihood
x <- planning(materiality = 0.03, likelihood = "poisson")
# Default beta prior and binomial likelihood
x <- planning(materiality = 0.03, likelihood = "binomial", prior = TRUE)
# Custom beta prior and binomial likelihood
x <- planning(materiality = 0.03, likelihood = "binomial", prior = prior)
summary(x)
## 
##  Bayesian Audit Sample Planning Summary
## 
## Options:
##   Confidence level:              0.95 
##   Materiality:                   0.03 
##   Hypotheses:                    H₀: Θ > 0.03 vs. H₁: Θ < 0.03 
##   Expected:                      0 
##   Likelihood:                    binomial 
##   Prior distribution:            beta(α = 1, β = 21) 
## 
## Results:
##   Minimum sample size:           78 
##   Tolerable errors:              0 
##   Posterior distribution:        beta(α = 1, β = 99) 
##   Expected most likely error:    0 
##   Expected upper bound:          0.029807 
##   Expected precision:            0.029807 
##   Expected BF₁₀:                 10.018

Selecting a sample

The selection() function is used to perform statistical selection of audit samples. It offers flexible implementations of the most common audit sampling algorithms for attributes sampling and monetary unit sampling. The function returns an object which can be used with associated summary() and plot() methods. For convenience, the input for the size argument can be an returned by the planning() function.

For additional details about this function, please refer to the function documentation on the package website.

Example usage:

# Fixed interval monetary unit sampling
x <- selection(
  data = BuildIt, size = 100, units = "values",
  method = "interval", values = "bookValue"
)
summary(x)
## 
##  Audit Sample Selection Summary
## 
## Options:
##   Requested sample size:         100 
##   Sampling units:                monetary units 
##   Method:                        fixed interval sampling 
##   Starting point:                1 
## 
## Data:
##   Population size:               3500 
##   Population value:              1403221 
##   Selection interval:            14032 
## 
## Results:
##   Selected sampling units:       100 
##   Proportion of value:           0.037014 
##   Selected items:                100 
##   Proportion of size:            0.028571

Evaluating a sample

The evaluation() function accepts a sample or summary statistics of the sample and performs evaluation according to the specified method. The function returns an object which can be used with associated summary() and plot() methods. To perform Bayesian evaluation, the input for the prior argument can be an object returned by the auditPrior() function, or an object returned by evaluation()$posterior.

For additional details about this function, please refer to the function documentation on the package website.

Example usage:

# Poisson likelihood
x <- evaluation(x = 1, n = 100, method = "poisson")
# Default beta prior and binomial likelihood
x <- evaluation(x = 1, n = 100, method = "binomial", prior = TRUE)
# Custom beta prior and binomial likelihood
x <- evaluation(x = 1, n = 100, method = "binomial", prior = prior)
summary(x)
## 
##  Bayesian Audit Sample Evaluation Summary
## 
## Options:
##   Confidence level:               0.95 
##   Method:                         binomial 
##   Prior distribution:             beta(α = 1, β = 21) 
## 
## Data:
##   Sample size:                    100 
##   Number of errors:               1 
##   Sum of taints:                  1 
## 
## Results:
##   Posterior distribution:         beta(α = 2, β = 120) 
##   Most likely error:              0.0083333 
##   95 percent credible interval:   [0, 0.038604] 
##   Precision:                      0.030271

Benchmarks

To ensure the accuracy of statistical results, jfa employs automated unit tests that regularly validate the output from the package against the following established benchmarks in the area of audit sampling:

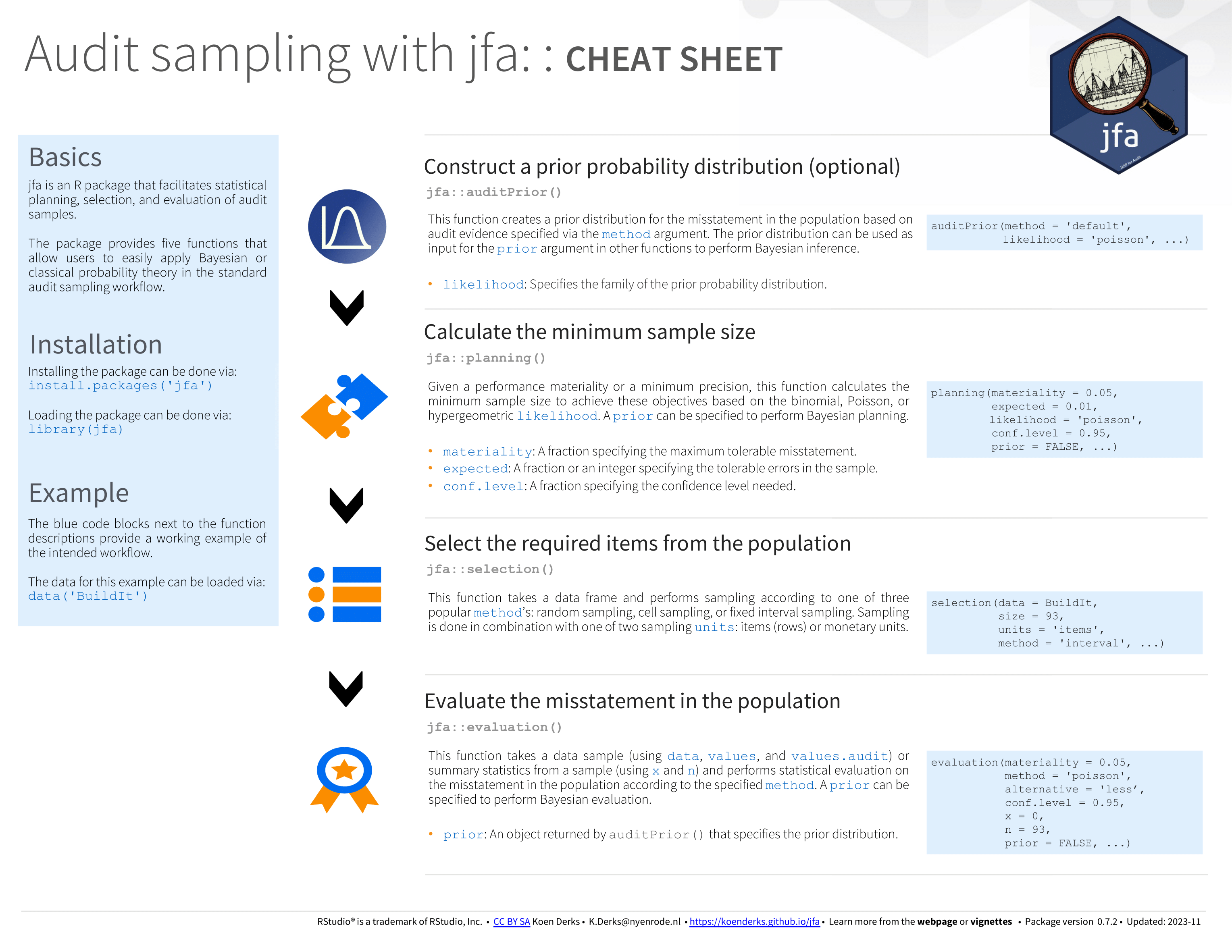
Cheat sheet

The cheat sheet below will help you get started with jfa’s intended audit sampling workflow. A pdf version can be downloaded here.

cheatsheet-sampling

References

American Institute of Certified Public Accountants (AICPA). (2021). Clarified statements on auditing standards. American Institute of Certified Public Accountants (AICPA).
International Auditing and Assurance Standards Board (IAASB). (2018). Handbook of international quality control, auditing review, other assurance, and related services pronouncements (vol. i). International Federation of Accountants.
Manitz, J., Hempelmann, M., Kauermann, G., Kuechenhoff, H., Shao, S., Oberhauser, C., Westerheide, N., & Wiesenfarth, M. (2021). Samplingbook: Survey sampling procedures. https://CRAN.R-project.org/package=samplingbook
Prömpers, H., & Guimarães, A. (2019). MUS: Monetary unit sampling and estimation methods, widely used in auditing. https://CRAN.R-project.org/package=MUS
Public Company Accounting Oversight Board (PCAOB). (2020). Auditing standards. Public Company Accounting Oversight Board (PCAOB).