Algorithm Auditing: Fairness Metrics and Parity

This function aims to assess fairness in algorithmic decision-making systems by computing and testing the equality of one of several model-agnostic fairness metrics between protected classes. The metrics are computed based on a set of true labels and the predictions of an algorithm. The ratio of these metrics between any unprivileged protected class and the privileged protected class is called parity. This measure can quantify potential fairness or discrimination in the algorithms predictions. Available parity metrics include predictive rate parity, proportional parity, accuracy parity, false negative rate parity, false positive rate parity, true positive rate parity, negative predicted value parity, specificity parity, and demographic parity. The function returns an object of class jfaFairness that can be used with associated summary() and plot() methods.

model_fairness(
  data,
  protected,
  target,
  predictions,
  privileged = NULL,
  positive = NULL,
  metric = c(
    "prp", "pp", "ap", "fnrp", "fprp",
    "tprp", "npvp", "sp", "dp"
  ),
  alternative = c("two.sided", "less", "greater"),
  conf.level = 0.95,
  prior = FALSE
)

Arguments

data: a data frame containing the input data.
protected: a character specifying the column name in data containing the protected classes (i.e., the sensitive attribute).
target: a character specifying the column name in data containing the true labels of the target (i.e., to be predicted) variable.
predictions: a character specifying the column name in data containing the predicted labels of the target variable.
privileged: a character specifying the factor level of the column protected to be used as the privileged group. If NULL (the default), the first factor level of the protected column is used.
positive: a character specifying the factor level positive class of the column target to be used as the positive class. If NULL (the default), the first factor level of the target column is used.
metric: a character indicating the fairness metrics to compute. See the Details section below for more information.
alternative: a character indicating the alternative hypothesis and the type of confidence / credible interval used in the individual comparisons to the privileged group. Possible options are two.sided (default), less, or greater. The alternative hypothesis relating to the overall equality is always two sided.
conf.level: a numeric value between 0 and 1 specifying the confidence level (i.e., 1 - audit risk / detection risk).
prior: a logical specifying whether to use a prior distribution, or a numeric value equal to or larger than 1 specifying the prior concentration parameter. If this argument is specified as FALSE (default), classical estimation is performed and if it is TRUE, Bayesian estimation using a default prior with concentration parameter 1 is performed.

Value

An object of class jfaFairness containing:

data: the specified data.
conf.level: a numeric value between 0 and 1 giving the confidence level.
privileged: The privileged group for computing the fairness metrics.
unprivileged: The unprivileged group(s).
target: The target variable used in computing the fairness metrics.
predictions: The predictions used to compute the fairness metrics.
protected: The variable indicating the protected classes.
positive: The positive class used in computing the fairness metrics.
negative: The negative class used in computing the fairness metrics.
alternative: The type of confidence interval.
confusion.matrix: A list of confusion matrices for each group.
performance: A data frame containing performance metrics for each group, including accuracy, precision, recall, and F1 score.
metric: A data frame containing, for each group, the estimates of the fairness metric along with the associated confidence / credible interval.
parity: A data frame containing, for each unprivileged group, the parity and associated confidence / credible interval when compared to the privileged group.
odds.ratio: A data frame containing, for each unprivileged group, the odds ratio of the fairness metric and its associated confidence/credible interval, along with inferential measures such as uncorrected p-values or Bayes factors.
measure: The abbreviation of the selected fairness metric.
prior: a logical indicating whether a prior distribution was used.
data.name: The name of the input data object.

Details

The following model-agnostic fairness metrics are computed based on the confusion matrix for each protected class, using the true positives (TP), false positives (FP), true negative (TN) and false negatives (FN). See Pessach & Shmueli (2022) for a more detailed explanation of the individual metrics. The equality of metrics across groups is done according to the methodology described in Fisher (1970) and Jamil et al. (2017).

Predictive rate parity (prp): calculated as TP / (TP + FP), its ratio quantifies whether the predictive rate is equal across protected classes.
Proportional parity (pp): calculated as (TP + FP) / (TP + FP + TN + FN), its ratio quantifies whether the positive prediction rate is equal across protected classes.
Accuracy parity (ap): calculated as (TP + TN) / (TP + FP + TN + FN), quantifies whether the accuracy is the same across groups.
False negative rate parity (fnrp): calculated as FN / (FP + FN), quantifies whether the false negative rate is the same across groups.
False positive rate parity (fprp): calculated as FP / (TN + FP), quantifies whether the false positive rate is the same across groups.
True positive rate parity (tprp): calculated as TP / (TP + FN), quantifies whether the true positive rate is the same across groups.
Negative predicted value parity (npvp): calculated as TN / (TN + FN), quantifies whether the negative predicted value is equal across groups.
Specificity parity (sp): calculated as TN / (TN + FP), quantifies whether the true positive rate is the same across groups.
Demographic parity (dp): calculated as TP + FP, quantifies whether the positive predictions are equal across groups.

Note that, in an audit context, not all fairness measures are equally appropriate in all situations. The fairness tree below aids in choosing which fairness measure is appropriate for the situation at hand (Büyük, 2023).

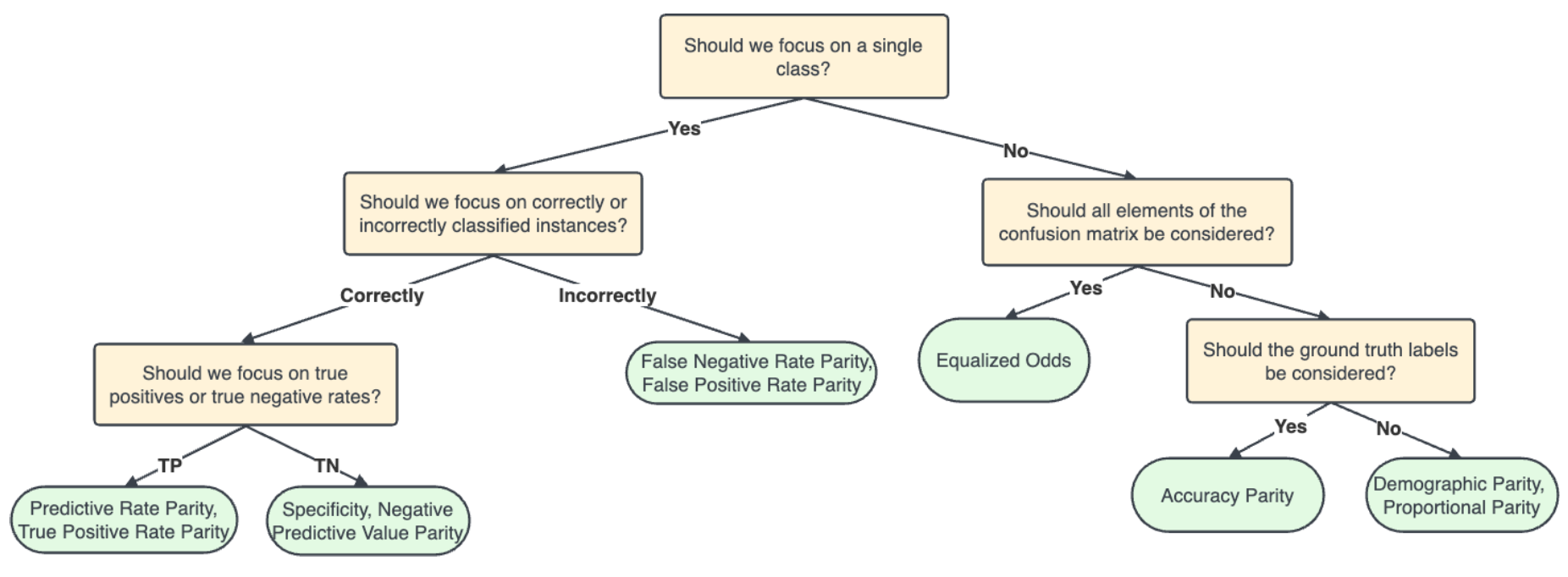
fairness-tree

References

Büyük, S. (2023). Automatic Fairness Criteria and Fair Model Selection for Critical ML Tasks, Master Thesis, Utrecht University.

Calders, T., & Verwer, S. (2010). Three naive Bayes approaches for discrimination-free classification. In Data Mining and Knowledge Discovery. Springer Science and Business Media LLC. doi:10.1007/s10618-010-0190-x

Chouldechova, A. (2017). Fair prediction with disparate impact: A study of bias in recidivism prediction instruments. In Big Data. Mary Ann Liebert Inc. doi:10.1089/big.2016.0047

Feldman, M., Friedler, S. A., Moeller, J., Scheidegger, C., & Venkatasubramanian, S. (2015). Certifying and removing disparate impact. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. doi:10.1145/2783258.2783311

Friedler, S. A., Scheidegger, C., Venkatasubramanian, S., Choudhary, S., Hamilton, E. P., & Roth, D. (2019). A comparative study of fairness-enhancing interventions in machine learning. In Proceedings of the Conference on Fairness, Accountability, and Transparency. doi:10.1145/3287560.3287589

Fisher, R. A. (1970). Statistical Methods for Research Workers. Oliver & Boyd.

Jamil, T., Ly, A., Morey, R. D., Love, J., Marsman, M., & Wagenmakers, E. J. (2017). Default "Gunel and Dickey" Bayes factors for contingency tables. Behavior Research Methods, 49, 638-652. doi:10.3758/s13428-016-0739-8

Pessach, D. & Shmueli, E. (2022). A review on fairness in machine learning. ACM Computing Surveys, 55(3), 1-44. doi:10.1145/3494672

Zafar, M. B., Valera, I., Gomez Rodriguez, M., & Gummadi, K. P. (2017). Fairness beyond disparate Ttreatment & disparate impact. In Proceedings of the 26th International Conference on World Wide Web. doi:10.1145/3038912.3052660

Author

Koen Derks, k.derks@nyenrode.nl

Examples

# Frequentist test of specificy parity
model_fairness(
  data = compas,
  protected = "Gender",
  target = "TwoYrRecidivism",
  predictions = "Predicted",
  privileged = "Male",
  positive = "yes",
  metric = "sp"
)
#> 
#> 	Classical Algorithmic Fairness Test
#> 
#> data: compas
#> n = 6172, X-squared = 121.26, df = 1, p-value < 2.2e-16
#> alternative hypothesis: fairness metrics are not equal across groups
#> 
#> sample estimates:
#>   Female: 1.3203 [1.2794, 1.3568], p-value = < 2.22e-16
#> alternative hypothesis: true odds ratio is not equal to 1